Suffix Automata
Συχνά σε διαγωνισμούς πληροφορικής (κυρίως στο ACM-ICPC αλλά από τώρα και στην IOI) εμφανίζονται προβλήματα τα οποία χρειάζονται ορισμένους αλγορίθμους σε αλφαριθμητικά για να λυθούν. Οι πιο περίπλοκοι όμως τέτοιοι αλγόριθμοι έχουν αρχίσει να εμφανίζονται τα τελευταία χρόνια, αν και υπήρχαν από πιο παλιά και χρησιμοποιούνταν κυρίως στα Linux. Μία από τις δυσκολότερες και ταυτόχρονα δυνατότερες δομές για αλφαριθμητικά είναι τα Suffix Automata. Τα Suffix Automata παρουσιάζουν μεγάλο ενδιαφέρον επειδή συνδυάζουν πολλές τεχνικές ταυτόχρονα εκτός από αλγορίθμους αλφαριθμητικών (θεωρία γράφων, δυναμικός προγραμματισμός).
- Ορισμός
- Παραδείγματα
- Σύνολο τερματικών θέσεων
- Επιθεματικοί σύνδεσμοι
- Συνοψίζοντας
- Κατασκευή
- Εφαρμογές
- Προβλήματα
- Πηγές
Ορισμός
To Suffix Automaton ενός αλφαριθμητικού καλείται ο κατευθυνόμενος μη κυκλικός γράφος, στον οποίο οι κορυφές καλούνται καταστάσεις και οι ακμές μεταξύ αυτών μεταβάσεις μεταξύ των καταστάσεων.
-
Μία από τις καταστάσεις καλείται η αρχική κατάσταση και πρέπει να είναι η πηγή (δηλαδή η κατάσταση που έχει πρόσβαση σε όλες τις άλλες).
-
Κάθε μετάβαση στη μηχανή είναι μια ακμή με ένα σύμβολο του αλφαβήτου μας για ένδειξη. Όλες οι μεταβάσεις που ξεκινούν από μια κατάσταση πρέπει να έχουν διαφορετικές ενδείξεις.
-
Μία ή περισσότερες καταστάσεις σημαδεύονται ως οι τερματικές καταστάσεις. Αν ξεκινήσουμε από την αρχική κατάσταση , ακολουθήσουμε ένα οποιοδήποτε μονοπάτι προς κάποια τερματική κατάσταση και καθ’ όλη τη διάρκεια της διαδρομής γράφουμε τις ενδείξεις των ακμών που διασχίζουμε τότε θα πάρουμε ένα αλφαριθμητικό το οποίο πρέπει να αποτελεί επίθεμα του .
-
Το Suffix Automaton περιλαμβάνει τον μικρότερο αριθμό κορυφών από όλους τους πιθανούς γράφους που μπορεί να δημιουργηθούν με βάση τις παραπάνω ιδιότητες.
Παραδείγματα
Ας δούμε μερικά Suffix Automata. Η αρχική κατάσταση θα συμβολίζεται με και οι τερματικές με .
-
Για το αλφαριθμητικό :

-
Για το αλφαριθμητικό :
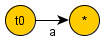
-
Για το αλφαριθμητικό :

-
Για το αλφαριθμητικό :
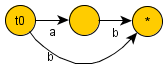
-
Για το αλφαριθμητικό :
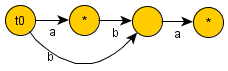
-
Για το αλφαριθμητικό :
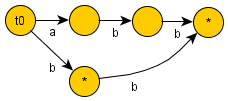
-
Για το αλφαριθμητικό :
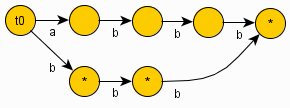
Σύνολο τερματικών θέσεων
Ας θεωρήσουμε το μη μηδενικό υπό-αλφαριθμητικό του . Ονομάζουμε το σύνολο όλων των θέσεων στο στις οποίες τελειώνει μια εμφάνιση του . Δύο αλφαριθμητικά ορίζονται ως ισοδύναμα αν τα σύνολα των τερματικών τους θέσεων είναι ίσα. Έτσι όλα τα μη μηδενικά υπο-αλφαριθμητικά μπορούν να χωριστούν σε ισοδύναμες κλάσεις σύμφωνα με τα σύνολα .
Π.χ. μερικά σύνολα του είναι (αν οι θέσεις ξεκινούν από το 0) :
Παρατηρήστε πως . Αυτό σημαίνει ότι τα δύο αυτά αλφαριθμητικά ανήκουν στην ίδια ισοδύναμη κλάση.
Προκύπτει ότι σε ένα Suffix Automaton όλα τα αλφαριθμητικά μιας ισοδύναμης κλάσης αντιστοιχούν στην ίδια κατάσταση. Με άλλα λόγια, ο αριθμός των καταστάσεων σε ένα Suffix Automaton ισούται με τον αριθμό των ισοδύναμων κλάσεων συν ένα (από την αρχική κατάσταση). Αποδεικνύεται όμως ότι στην χειρότερη περίπτωση θα υπάρχουν το πολύ διαφορετικές καταστάσεις!!! Αυτή την πρόταση θα την θεωρήσουμε δεδομένη. Ακολουθούν κάποιες απλές αλλά χρήσιμες προτάσεις σχετικά με τα σύνολα .
Λήμμα 1: Δύο μη μηδενικά υπο-αλφαριθμητικά και με είναι ισοδύναμα αν και μόνο αν οπουδήποτε υπάρχει το στο αποτελεί επίθεμα του .
Η απόδειξη είναι σχεδόν προφανής: Για την απλή συνεπαγωγή, ισχύει ότι αφού το και το τελειώνουν στις ίδιες θέσεις στο τότε αναγκαστικά το ένα (μικρότερο) θα είναι επίθεμα του άλλου. Αντίστροφα, αν το εμφανίζεται στο μόνο σαν επίθεμα του τότε από τον ορισμό ξέρουμε ότι το τελειώνει στις ακριβώς ίδιες θέσεις με το .
Λήμμα 2: Ας θεωρήσουμε ξανά δύο μη μηδενικά υπο-αλφαριθμητικά και με . Τότε τα σύνολά τους είναι είτε ξένα μεταξύ τους είτε το περιέχεται πλήρως στο , το οποίο εξαρτάται από το αν το είναι επίθεμα του ή όχι.
Για παράδειγμα το περιέχεται πλήρως στο αφού το είναι επίθεμα του .
Απόδειξη: Ας υποθέσουμε ότι τα σύνολα και έχουν τουλάχιστον ένα κοινό στοιχείο. Τότε αυτό σημαίνει ότι τα αλφαριθμητικά τελειώνουν στην ίδια θέση, δηλαδή το είναι επίθεμα του . Αλλά τότε σε κάθε του εμφάνιση, το περιέχει στο τέλος του το , κάτι που σημαίνει ότι το περιέχεται πλήρως στο .
Λήμμα 3: Αν ταξινομήσουμε όλα τα υπο-αλφαριθμητικά σε μια ισοδύναμη κλάση κατά φθίνουσα σειρά μηκών, τότε στην τελική ακολουθία κάθε υπο-αλφαριθμητικό θα είναι μικρότερο του προηγούμενου και ταυτόχρονα θα είναι επίθεμά του. Με άλλα λόγια, τα υπο-αλφαριθμητικά που περιέχονται σε μια ισοδύναμη κλάση είναι επιθέματα μεταξύ τους και έχουν όλα τα πιθανά μήκη σε ένα διάστημα .
Για παράδειγμα, αν εφαρμόσουμε την παραπάνω διαδικασία στην κλάση του προηγούμενου παραδείγματος θα πάρουμε την ακολουθία με μήκη στο .
Απόδειξη: Έστω μια ισοδύναμη κλάση. Αν περιέχει μόνο ένα αλφαριθμητικό τότε το Λήμμα είναι προφανώς σωστό. Ας υποθέσουμε τώρα ότι ο αριθμός των αλφαριθμητικών είναι μεγαλύτερος. Σύμφωνα με το Λήμμα 1, δύο αλφαριθμητικά σε μια ισοδύναμη κλάση είναι πάντα τέτοια ώστε το ένα να είναι επίθεμα του άλλου. Έτσι, σε μια ισοδύναμη κλάση δεν μπορούν να υπάρχουν αλφαριθμητικά ίδιου μεγέθους. Ας υποθέσουμε λοιπόν ότι το είναι το αλφαριθμητικό με το μεγαλύτερο μήκος σε ένα σύνολο και το είναι αυτό με το μικρότερο μήκος. Σύμφωνα με το Λήμμα 1, το είναι επίθεμα του . Τώρα ας θεωρήσουμε ένα οποιοδήποτε επίθεμα του με μήκος στο διάστημα . Θα δείξουμε ότι ανήκει στην ίδια ισοδύναμη κλάση με το . Στην πραγματικότητα το αλφαριθμητικό αυτό μπορεί να υπάρξει στο μόνο ως επίθεμα του αφού το μικρότερο επίθεμά του που υπάρχει μόνο ως επίθεμά του είναι το . Έτσι, ξανά σύμφωνα με το Λήμμα 1, αυτό το αλφαριθμητικό ανήκει στην ίδια ισοδύναμη τάξη με τα άλλα δύο.
Επιθεματικοί σύνδεσμοι
Ας θεωρήσουμε μία κατάσταση στο Suffix Automaton διαφορετική της . Όπως τώρα γνωρίζουμε, η αντιστοιχεί σε μία συγκεκριμένη ισοδύναμη κλάση αλφαριθμητικών που χαρακτηρίζεται από το σύνολό της, έτσι αν συμβολίσουμε με το αλφαριθμητικό με το μεγαλύτερο μήκος εκεί, τότε όλα τα υπόλοιπα θα είναι επιθέματα του . Ξέρουμε επίσης ότι τα πρώτα μερικά μεγαλύτερα επιθέματα του ανήκουν επίσης στην ίδια ισοδύναμη κλάση ενώ όλα τα υπόλοιπα (τουλάχιστον το κενό) σε διαφορετικές. Ας συμβολίσουμε με την κλάση του μεγαλύτερου επιθέματος του που δεν ανήκει στην ίδια ισοδύναμη κλάση με αυτό. Προς αυτή θα βάλουμε έναν επιθεματικό σύνδεσμο (ή αλλιώς Suffix Link) και θα τον γράφουμε .
Θα υποθέτουμε στη συνέχεια ότι η αρχική κατάσταση αντιστοιχεί σε μία ισοδύναμη κλάση, η οποία περιέχει μόνο ένα κενό αλφαριθμητικό και ισχύει .
Παρακάτω υπάρχει ένα παράδειγμα του Suffix Automaton (αριστερά) και των Suffix Links του (δεξιά) από το αλφαριθμητικό .
Παρατηρήστε πως τα ανήκουν στην ίδια κλάση και ότι το μεγαλύτερο επίθεμα του που δεν ανήκει στην κλάση αυτή είναι το στο οποίο καταλήγει και το αντίστοιχο suffix link.
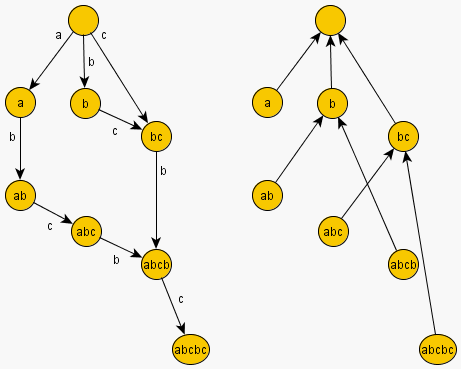
Λήμμα 4: Οι επιθεματικοί σύνδεσμοι (όπως φαίνεται και στο προηγούμενο παράδειγμα) σχηματίζουν ένα δέντρο, η ρίζα του οποίου είναι η αρχική κατάσταση .
Απόδειξη: Θεωρούμε μια αυθαίρετη κατάσταση . Ακολουθώντας τα suffix links από αυτή τη κατάσταση θα καταλήξουμε κάποτε στο που αντιστοιχεί στο κενό αλφαριθμητικό, αφού οι επιθεματικοί σύνδεσμοι καταλήγουν πάντα σε αλφαριθμητικά με γνησίως μικρότερο μήκος (αυτό προκύπτει από τον ορισμό των επιθεματικών συνδέσμων και το Λήμμα 3).
Λήμμα 5: Αν κατασκευάσουμε το δέντρο των έτσι ώστε κάθε κόμβος να είναι υποσύνολο κάθε προγόνου του, τότε θα έχουμε το ίδιο δέντρο που παίρνουμε από τα suffix links.
Απόδειξη: Είναι γεγονός ότι τα σύνολα μπορούν να κατασκευάσουν ένα δέντρο, γιατί όπως γνωρίζουμε από το Λήμμα 2, κάθε δύο σύνολα είναι είτε ξένα μεταξύ τους είτε το ένα περιέχεται στο άλλο. Τώρα ας θεωρήσουμε μια οποιαδήποτε κατάσταση και τον επιθεματικό της σύνδεσμο . Από τον ορισμό των επιθεματικών συνδέσμων και το Λήμμα 2 προκύπτει ότι , το οποίο μαζί και με το Λήμμα 4 αποδεικνύουν τον ισχυρισμό μας.
Συνοψίζοντας
Προτού προχωρήσουμε στην περιγραφή του αλγορίθμου κατασκευής, θα συνοψίσουμε τα παραπάνω και θα εισάγουμε ορισμένους νέους συμβολισμούς.
-
Όλα τα υπο-αλφαριθμητικά ενός αλφαριθμητικού μπορούν να διαιρεθούν σε κάποιες κλάσεις ισοδυναμίας σύμφωνα με το σύνολο των τερματικών τους θέσεων μέσα στο .
-
Ένα Suffix Automaton αποτελείται από την αρχική κατάσταση καθώς και από ένα κόμβο για κάθε ισοδύναμη κλάση. Συνολικά θα υπάρχουν το πολύ καταστάσεις!!!
-
Κάθε κατάσταση αντιστοιχεί σε ένα ή περισσότερα αλφαριθμητικά. Ας συμβολίσουμε με το αλφαριθμητικό της με το μεγαλύτερο μήκος και με αυτό με το μικρότερο μήκος και , τα μήκη τους αντίστοιχα. Τότε όλα τα αλφαριθμητικά που αντιστοιχούν σε αυτή την κατάσταση έχουν μήκος στο διάστημα .
-
Για κάθε κατάσταση ορίζεται ένας επιθεματικός σύνδεσμος που οδηγεί στην κατάσταση που αντιστοιχεί στο επίθεμα του με μήκος . Οι επιθεματικοί σύνδεσμοι σχηματίζουν ένα δέντρο με ρίζα το στο οποίο το του κάθε κόμβου είναι η ένωση όλων των παιδιών του.
-
Έτσι το μπορεί να βρεθεί ως εξής: .
-
Αν ξεκινήσουμε από μία αυθαίρετη κατάσταση και ακολουθήσουμε τους επιθεματικούς συνδέσμους θα καταλήξουμε αργά ή γρήγορα στην αρχική κατάσταση . Επιπλέον καθώς ακολουθούμε τους συνδέσμους παίρνουμε μη επικαλυπτόμενα διαστήματα των οποίων η ένωση αποτελεί ένα ενιαίο διάστημα.
Κατασκευή
Στη συνέχεια παρουσιάζουμε έναν online αλγόριθμο κατασκευής του Suffix Automaton ενός αλφαριθμητικού, που σημαίνει ότι θα το μεταβάλλουμε με κάθε νέο χαρακτήρα. Συνολικά ο αλγόριθμος είναι γραμμικός. Για να καταφέρουμε να καταναλώνουμε γραμμική μνήμη θα αποθηκεύουμε σε κάθε κατάσταση μόνο τις τιμές των len, link και τη λίστα των μεταβάσεων από αυτή την κατάσταση.
struct state {
int len, link;
map<char, int> delta;
// Το map προσθέτει έναν επιπλέον log(k) παράγοντα,
// αλλά θα μπορούσε να αντικατασταθεί με ένα hash table.
} st[2 * MAX_N]; // θυμηθείτε πως υπάρχουν το πολύ 2 * Ν καταστάσεις
Αρχικά, το Automaton αποτελείται μόνο από την αρχική κατάσταση, την οποία θα θεωρούμε την κατάσταση 0 (ενώ τις υπόλοιπες 1,2,3,…). Το len της θα ισούται με 0 και το link της, για άνεση, με -1 (μία φανταστική κατάσταση). Οπότε πριν από οτιδήποτε άλλο θα πρέπει να καλέσουμε την συνάρτηση init_sa() για να αρχικοποιήσει αυτές τις μεταβλητές.
int last, sz;
void init_sa() {
last = 0;
sz = 1;
st[last].len = 0;
st[last].link = -1;
st[last].delta.clear();
}
Τώρα αυτό που μένει είναι να καταλάβουμε πώς αλλάζει η δομή όταν προσθέσουμε έναν νέο χαρακτήρα c στο τέλος του αλφαριθμητικού. Ακολουθεί η διαδικασία:
-
Υποθέτουμε ότι η
lastείναι η τελευταία κατάσταση που προσθέσαμε, η οποία αντιστοιχεί σε ολόκληρο το αλφαριθμητικό. (Αρχικά ηlastισούται με 0) -
Δημιουργούμε μία νέα κατάσταση
curκαι θέτουμε τοlen(cur)να είναι ίσο μεlen(last)+1. Προς το παρόν τοlink(cur)είναι αόριστο.
int cur = sz++;
st[cur].len = st[last].len + 1;
st[cur].delta.clear();
- Ακολουθούμε την εξής διαδικασία: Αρχικά είμαστε στο
last. Όσο δεν υπάρχει μετάβαση από την τρέχουσα κατάσταση με τον χαρακτήραcτότε την προσθέτουμε προς τοcur(αυτό σημαίνει ότι όλα τα επιθέματα τουSστην τρέχουσα κλάση μπορούν να μετασχηματιστούν με την προσθήκη τουcσε επιθέματα τουS+cκαι να ανήκουν στην κλάσηcur) και ακολουθούμε τους επιθεματικούς συνδέσμους μέχρι να φτάσουμε σε μια κατάσταση που ήδη έχει μετάβαση με τονcή στην -1.
for (p = last; p != -1 && !st[p].delta.count(c); p = st[p].link)
st[p].delta[c] = cur;
-
Αν με την προηγούμενη διαδικασία καταλήξαμε στην φανταστική κατάσταση -1, που σημαίνει ότι δεν φεύγει μετάβαση με τον χαρακτήρα
cαπό καμία κατάσταση στη διαδρομή μας, τότε θέτουμεlink(cur) = 0και σταματάμε τον αλγόριθμο προσθήκης νέου χαρακτήρα. -
Ας υποθέσουμε τώρα ότι σταματήσαμε σε μια κατάσταση
p, από την οποία υπάρχει μετάβαση με τονc. Ας συμβολίσουμε μεqτην κατάσταση στην οποία οδηγεί αυτή η μετάβαση. -
Τώρα υπάρχουν δύο περιπτώσεις σύμφωνα με το αν
len(p) + 1 = len(q)ή όχι. -
Αν ισχύει τότε μπορούμε απλά να θέσουμε
link(cur) = qκαι να σταματήσουμε (Σκεφτείτε γιατί ισχύει αυτό πριν προχωρήσετε!). -
Διαφορετικά (αν
len(p) + 1 < len(q)) προκειμένου να “εξομοιώσουμε” την προηγούμενη περίπτωση κατασκευάζουμε μία κατάσταση κλώνο τουq, ας την πούμε “clone”. Για να την δημιουργήσουμε αντιγράφουμε όλες τις μεταβάσεις από τηνqκαθώς και τον επιθεματικό σύνδεσμο. Θέτουμε όμωςlen(clone) = len(p) + 1. Μετά την κλωνοποίηση θέτουμε τοlink(cur)αλλά και τοlink(q)να είναι ίσα με τοclone. Τέλος, ακολουθώντας τους επιθεματικούς συνδέσμους από τοpελέγχουμε αν υπάρχει μετάβαση από την τρέχουσα κατάσταση στοq, αν ναι τότε την συνδέουμε στοcloneκαι αν όχι σταματάμε.
void sa_extend(char c) {
int cur = sz++;
st[cur].len = st[last].len + 1;
st[cur].delta.clear();
int p;
for (p = last; p != -1 && !st[p].delta.count(c); p = st[p].link)
st[p].delta[c] = cur;
if (p == -1)
st[cur].link = 0;
else {
int q = st[p].delta[c];
if (st[p].len + 1 == st[q].len)
st[cur].link = q;
else {
int clone = sz++;
st[clone].delta = st[q].delta;
st[clone].link = st[q].link;
st[clone].len = st[p].len + 1;
for (; p != -1 && st[p].delta[c] == q; p = st[p].link)
st[p].delta[c] = clone;
st[q].link = st[cur].link = clone;
}
}
last = cur;
}
Συνιστούμε να εξομοιώσετε στο χαρτί τον αλγόριθμο με κάποια από τα αλφαριθμητικά των παραδειγμάτων και να ελέγξετε αν το Suffix Automaton βγήκε ίδιο με των εικόνων έτσι ώστε να σιγουρευτείτε ότι είναι ξεκάθαρη η διαδικασία!
Αν θέλουμε να σημαδέψουμε με κάποιον τρόπο τις τερματικές καταστάσεις, τότε ξεκινώντας από την τελευταία κατάσταση που προσθέσαμε και ακολουθώντας όλους τους επιθεματικούς συνδέσμους σημαδεύουμε όλες τις καταστάσεις που συναντήσαμε ως τερματικές (συμπεριλαμβανομένης της τελικής). Είναι προφανές ότι έτσι έχουμε καλύψει όλα τα επιθέματα του αλφαριθμητικού μας.
for (int p = last; p != 0; p = st[p].link)
terminal[p] = true;
Εφαρμογές
Αυτό είναι ίσως το πιο ενδιαφέρον κομμάτι των Suffix Automata αφού μας επιτρέπουν να μετατρέψουμε προβλήματα αλφαριθμητικών σε προβλήματα γράφων. Μάλιστα το γεγονός ότι αποτελούν DAGs μας δίνει συχνά τη δυνατότητα να εφαρμόσουμε αλγορίθμους δυναμικού προγραμματισμού πάνω σε αυτά!
Συνιστούμε να προσπαθήσετε να λύσετε τα επόμενα προβλήματα από μόνοι σας πριν δείτε τις λύσεις.
Υπάρχει ένα δοσμένο αλφαριθμητικό μέσα σε ένα άλλο ;
Λύση: Αυτό το πρόβλημα είναι πολύ απλό αφού το μόνο που έχουμε να κάνουμε είναι να διατρέξουμε το Suffix Automaton του από την αρχική κατάσταση και να ελέγξουμε αν μπορούμε μέσα από διαδοχικές μεταβάσεις να σχηματίσουμε το .
bool is_substring(const string &w) {
int node = 0;
for (int i = 0; i < (int)w.size(); i++) {
if (!st[node].delta.count(w[i]))
return false;
node = st[node].delta[w[i]];
}
return true;
}
Είναι το επίθεμα του ;
Λύση: Αυτό είναι ένα εξίσου απλό πρόβλημα με το προηγούμενο, με την μόνη διαφορά ότι πρέπει να ελέγξουμε αν η τελευταία μας κατάσταση είναι τερματική ή όχι.
Ποιο είναι το πλήθος των διαφορετικών υπο-αλφαριθμητικών του ;
Λύση: Ο αριθμός αυτός ισούται με το πλήθος των διαφορετικών μονοπατιών στον γράφο μας ξεκινώντας από την αρχική κατάσταση. Αυτό είναι ένα πρόβλημα που μπορεί να λυθεί με τη χρήση δυναμικού προγραμματισμού. Η απάντηση για τον κόμβο ισούται με το άθροισμα όλων των τέτοια ώστε να υπάρχει ακμή από το στο συν 1 (για το μονοπάτι που σταματάει στο ).
void dfs(int u) {
if (visit[u]) return;
visit[u] = true;
dp[u] = 1;
for (auto v : st[u].delta) {
dfs(v.second);
dp[u] += dp[v.second];
}
}
Πόσες φορές εμφανίζεται το στο ;
Λύση: Οποιοδήποτε υπο-αλφαριθμητικό αποτελεί πρόθεμα ενός επιθέματος του ! Έτσι μπορούμε να προχωρήσουμε στους κόμβους του Suffix Automaton του μέχρι να φτάσουμε σε αυτόν που αντιστοιχεί στο , ας πούμε στον . Στη συνέχεια (με όμοιο τρόπο με το τελευταίο πρόβλημα) μας ενδιαφέρει να ξέρουμε πόσα επιθέματα του μπορούμε να καλύψουμε αν συνεχίσουμε την διαδρομή μας (δηλαδή πόσων επιθεμάτων αποτελεί το πρόθεμα). Για αυτόν τον λόγο αρκεί να επιστρέψουμε το πλήθος των μονοπατιών που ξεκινούν από το και τελειώνουν σε μία τερματική κατάσταση.
Που εμφανίζεται για πρώτη φορά το μέσα στο ;
Λύση: Το πρόβλημα είναι ισοδύναμο με το να υπολογίσουμε το μακρύτερο μονοπάτι που ξεκινάει από το (όπως ορίστηκε στη προηγούμενη λύση) και τελειώνει σε κάποια τερματική κατάσταση. Έτσι έχουμε βρει ποια είναι η μέγιστη δυνατή απόσταση από το τέλος του προθέματος (ίσου με ) ενός επιθέματος του προς το τέλος του .
Σε ποιες θέσεις του εμφανίζεται το ;
Πρώτη Λύση: Όπως και στα προηγούμενα προβλήματα μπορούμε να διατρέξουμε το Automaton του μέχρι να φτάσουμε στο . Στη συνέχεια αρκεί να κάνουμε μία DFS από εκεί και να υπολογίσουμε όλες τις αποστάσεις του από κάποια τερματική κατάσταση (δηλαδή τις αποστάσεις μιας εμφάνισης του από το τέλος του ).
Αξίζει όμως να αναφέρουμε άλλη μία ενδιαφέρουσα λύση η οποία χρησιμοποιεί τα suffix links.
Δεύτερη Λύση: Αρχικά κατασκευάζουμε το δέντρο που σχηματίζεται από τα suffix links.
tree = vector<vector<int> >(sz);
for (int i = 0; i < sz; i++)
if (st[i].link >= 0)
tree[st[i].link].push_back(i);
Ύστερα εφαρμόζουμε την ίδια διαδικασία με πριν και φτάνουμε στον κόμβο . Από αυτόν αρκεί να τρέξουμε μια DFS στο δέντρο μέχρι να φτάσουμε στα φύλλα. Το θα εμφανίζεται τόσες φορές όσες είναι τα φύλλα που συναντήσαμε και χρησιμοποιώντας το len των φύλλων αυτών μπορούμε να προσδιορίσουμε και τις θέσεις στις οποίες τελειώνει μια εμφάνισή του.
Προβλήματα
Πηγές
e-maxx Suffix Automata (μέσω google translate)
codeforces A Short Guide to Suffix Automata