Γέφυρες και Κομβικά Σημεία
Οι αλγόριθμοι εύρεσης γεφυρών (bridges) και κομβικών σημείων (articulation points) μπορεί να φανούν ιδιαίτερα χρήσιμοι σε αρκετά προβλήματα Θεωρίας Γράφων. Εξίσου σημαντική όμως είναι και η τεχνική που χρησιμοποιούμε για να αποδείξουμε τους αλγορίθμους αυτούς. Μέχρι το 2017 οι αλγόριθμοι αυτοί δεν συμπεριλαμβάνονταν στην ύλη της IOI. Τώρα όμως περιλαμβάνονται και θεωρούνται βασική γνώση που όλοι οι διαγωνιζόμενοι πρέπει να κατέχουν.
Ορισμός
Για να δώσουμε τον ορισμό των γεφυρών και κομβικών σημείων θα πρέπει πρώτα να εξηγήσουμε τι είναι οι συνεκτικές συνιστώσες (connected components). Μια συνεκτική συνιστώσα, λοιπόν, ενός μη κατευθυνόμενου γράφου με κορυφές στο σύνολο και ακμές στο σύνολο , είναι ένας μέγιστος συνδεδεμένος υπο-γράφος του . Είναι δηλαδή ένας υπο-γράφος στον οποίο υπάρχει κάποιο μονοπάτι μεταξύ κάθε ζεύγους κορυφών αλλά δεν συνδέεται σε καμία άλλη κορυφή του γράφου .
(Είναι δηλαδή ένας μη κατευθυνόμενος γράφος του οποίου το σύνολο των κορυφών του είναι υποσύνολο του και το σύνολο των ακμών του είναι υποσύνολο του έτσι ώστε να υπάρχει ένα μονοπάτι μεταξύ κάθε ζεύγους κορυφών του και τα σύνολα των κορυφών και τον ακμών του να είναι τα μέγιστα δυνατά.)
Μπορείτε να βρείτε τις συνεκτικές συνιστώσες στον γράφο που ακολουθεί;
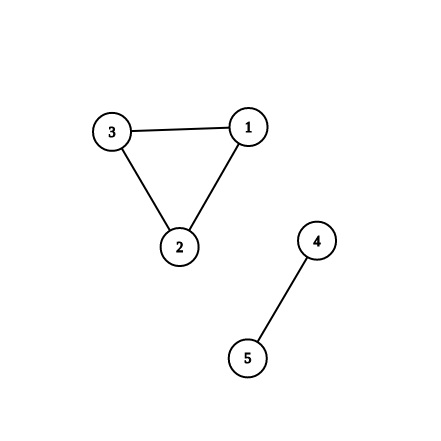
Ο γράφος αυτός έχει δύο συνεκτικές συνιστώσες, τις , . Η δεν θα μπορούσε να είναι συνεκτική συνιστώσα επειδή υπάρχουν τουλάχιστον δύο κορυφές που δεν συνδέονται μεταξύ τους και η δεν είναι επειδή δεν είναι η μέγιστη δυνατή, δεν περιλαμβάνει δηλαδή και το .
Τώρα θα μιλήσουμε για κομβικά σημεία και γέφυρες μη κατευθυνόμενων γράφων.
Κομβικά σημεία ενός μη κατευθυνόμενου γράφου καλούνται οι κορυφές εκείνες, οι οποίες όταν αφαιρεθούν οδηγούν στην αύξηση των συνεκτικών συνιστωσών του γράφου.
Γέφυρες ενός μη κατευθυνόμενου γράφου καλούνται οι ακμές οι οποίες όταν αφαιρεθούν αυξάνουν τις συνεκτικές συνιστώσες του γράφου.
Ποιες κορυφές και ποιες ακμές του ακόλουθου γράφου είναι κομβικά σημεία και γέφυρες αντίστοιχα;
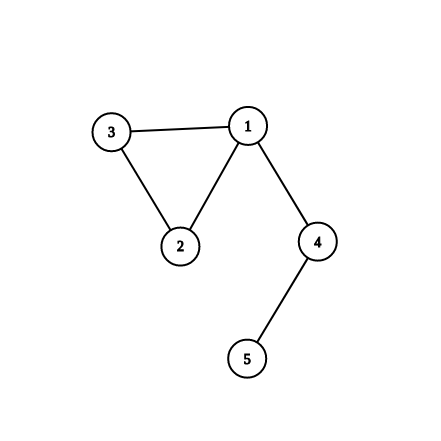
Κομβικά σημεία είναι το 1 (αφού όταν διαγραφτεί χωρίζει τον γράφο στις συνιστώσες και ) και το 4 (αφού όταν διαγραφτεί χωρίζει τον γράφο στις και ).
Γέφυρες είναι οι ακμές 1-4 (χωρίζει τον γράφο σε και ) και 4-5 (χωρίζει τον γράφο σε και ).
Προσέξτε ότι δεν είναι αναγκαστικά όλες οι γειτονικές ακμές ενός κομβικού σημείου γέφυρες και ούτε οι κορυφές μιας γέφυρας κομβικά σημεία!
Αλγόριθμος εύρεσης γεφυρών και κομβικών σημείων
Προτείνουμε να προσπαθήσετε να σκεφτείτε μια απλή λύση στο πρόβλημα μόνοι σας πριν προχωρήσετε έτσι ώστε να αποκτήσετε μια καλύτερη αίσθηση του θέματος.
Brute Force
Μία πολύ απλή λύση για να βρούμε τα κομβικά σημεία θα ήταν να δοκιμάσουμε να αφαιρέσουμε όλες τις κορυφές μία μία και μετά να ελέγχουμε αν ο αριθμός των συνεκτικών συνιστωσών αυξάνεται. Όμοια μπορούμε να δοκιμάσουμε να αφαιρούμε τις ακμές μία μία για να ελέγξουμε αν είναι γέφυρες. Ο αλγόριθμος αυτός έχει πολυπλοκότητα στη περίπτωση των κομβικών σημείων και στη περίπτωση των γεφυρών, όπου το είναι το πλήθος των κορυφών και το πλήθος των ακμών.
Υπάρχει όμως και καλύτερη λύση
Γραμμικός Αλγόριθμος
Ο John Hopcroft και ο Robert Tarjan έλυσαν το ίδιο πρόβλημα σε χρονική πολυπλοκότητα . Για αυτό χρησιμοποίησαν τις ιδιότητες του DFS-δέντρου του γράφου. Το DFS-tree ενός γράφου είναι το δέντρο που σχηματίζει η DFS ξεκινώντας από μια τυχαία κορυφή (από κάθε κορυφή υπάρχει και διαφορετικό δέντρο). Δηλαδή μια ακμή u-v υπάρχει στο δέντρο αν και μόνο αν η DFS την χρησιμοποίησε στην προσπέλαση του γράφου. Για παράδειγμα, όπως φαίνεται στην παρακάτω εικόνα, αν ξεκινήσουμε από την κορυφή 5 του γράφου (αριστερά) και εφαρμόσουμε τον αλγόριθμο της DFS τότε δεξιά φαίνεται ένα πιθανό DFS-δέντρο που θα μπορούσε να προκύψει.
Σημείωση: Εδώ χρησιμοποιούμε κατευθυνόμενες ακμές για να δείξουμε τη σειρά με την οποία περνάει η DFS από τους κόμβους.
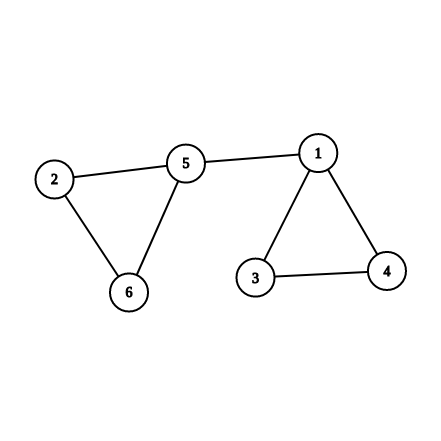
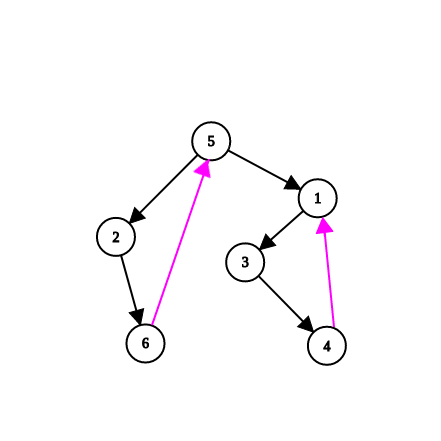
Παρατηρήστε πως οι μοβ ακμές δεν περιλαμβάνονται στο δέντρο αλλά είναι ιδιαίτερα χρήσιμες σε αρκετές περιπτώσεις. Αυτές καλούνται back edges επειδή είναι ακμές που δείχνουν από έναν κόμβο στους προγόνους του στο DFS-δέντρο. Οι υπόλοιπες ακμές - αυτές δηλαδή που περιέχονται στο δέντρο - ονομάζονται forward edges και δείχνουν από έναν κόμβο στους απογόνους του.
Θα ορίσουμε στη συνέχεια μερικές ακόμη ποσότητες που θα χρειαστούμε για να κατασκευάσουμε τον αλγόριθμο.
parείναι ένας πίνακας στον οποίο τοpar[u]έχει την τιμή του “πατέρα” τουuστο δέντρο ή την τιμή-1σε περίπτωση που οuείναι η ρίζα.numείναι ένας πίνακας ο οποίος περιέχει τον χρόνο (δηλαδή σε ποιο κάλεσμα) έφτασε η DFS στον αντίστοιχο κόμβο ή περιέχει την τιμή-1αν δεν έχουμε επισκεφτεί ακόμα τον κόμβο. Υπολογίζεται από την global μεταβλητήcounterπου αρχικά είναι μηδέν και αυξάνεται κατά 1 σε κάθε κλήση της DFS.lowείναι επίσης ένας πίνακας ο οποίος κρατάει τον χρόνο του “αρχαιότερου” κόμβου στο δέντρο στο οποίο οuμπορεί να φτάσει ακολουθώντας κάποιο μονοπάτι από forward edges και τελικά κάποιο back edge. Τοlow[u]είναι και αυτό-1αν δεν έχουμε επισκεφτεί ακόμα τονu.
Για παράδειγμα, στην προηγούμενη εικόνα, το low[4] θα είναι ίσο με το num[1] αφού αυτό είναι το μικρότερο που μπορεί να συναντήσει, το low[2] θα είναι το num[5] (οδηγείται εκεί μέσω του μονοπατιού 2-6-5) και το low[1] είναι το num[1] αφού όποιο μονοπάτι και να ακολουθήσει ο 1 προς τους απογόνους του και όποιο back edge και αν χρησιμοποιήσει θα καταλήγει πάντα σε κόμβους με num μεγαλύτερο από το δικό του.
Αφού έχουμε ορίσει όλα αυτά, μπορούμε εύκολα να κατασκευάσουμε τον αλγόριθμο. Αρκεί να κάνουμε μερικούς ελέγχους για κύκλους καθώς τρέχει η DFS. Συγκεκριμένα, μας ενδιαφέρει να κοιτάξουμε αν από έναν κόμβο u, υποψήφιο για κομβικό σημείο, υπάρχει μονοπάτι που οδηγεί πίσω από αυτόν στο DFS-δέντρο. Σε αυτή την περίπτωση ο κόμβος u δεν είναι κομβικό σημείο αφού αναγκαστικά θα βρίσκεται σε κύκλο. Αυτό μπορούμε εύκολα να το ελέγξουμε συγκρίνοντας το low[v] με το num[u]. Αν low[v] < num[u] τότε υπάρχει κύκλος (ο v μπορεί να φτάσει σε έναν πρόγονο του u ακολουθώντας κάποιο back edge) ενώ αν low[v] > num[u] τότε ο u θα είναι κομβικό σημείο. Ιδιαίτερη προσοχή απαιτείται βέβαια στη περίπτωση που που low[v] == num[u]. Αυτό σημαίνει ότι ο v ακολουθώντας κάποιο μονοπάτι μπορεί να φτάσει στον u με κάποιο back edge. Αν ο u έχει προγόνους τότε θα είναι κομβικό σημείο διότι θα αποσυνδέσει τους προγόνους του με τους απογόνους του σε περίπτωση που διαγραφεί. Αν όμως ο u δεν έχει απογόνους (δηλαδή είναι η ρίζα του DFS-δέντρου) τότε δεν είναι αναγκαστικό ότι θα αποσυνδέσει τον γράφο. Για να γίνει αυτό θα πρέπει να έχει τουλάχιστον δύο παιδιά, δηλαδή να φεύγουν τουλάχιστον δύο forward edges από αυτόν. Αυτό ακριβώς πετυχαίνουμε στον κώδικα που ακολουθεί με τη μεταβλητή kids, η οποία μετράει το πλήθος των forward edges από τον u.
Η περίπτωση με τις γέφυρες είναι ευκολότερη. Αν μία ακμή δεν ανήκει στο δέντρο τότε σίγουρα δεν είναι γέφυρα. Διαφορετικά, αρκεί (όμοια με πριν) να ισχύει low[v] > num[u] αφού αυτό θα σημαίνει ότι ο χαμηλότερος κόμβος στον οποίο μπορεί να φτάσει ο v βρίσκεται σίγουρα μετά τον u (είναι απόγονος του).
Ακολουθεί ο κώδικας:
vector<int> gr[MAXN];
int num[MAXN], low[MAXN], par[MAXN];
int counter = 0;
void dfs(int u) {
low[u] = num[u] = counter++;
int kids = 0;
for (auto v : gr[u]) {
if (num[v] == -1) {
// Εδώ υπάρχει forward edge.
par[v] = u;
dfs(v);
kids++;
// Όταν ο u είναι η ρίζα δεν έχει προγόνους.
// Άρα το par[u] θα πρέπει να ισούται με -1.
if (par[u] == -1 && kids > 1)
printf("articulation point - %d\n", u);
// Η περίπτωση για τις υπόλοιπες κορυφές.
if (par[u] != -1 && low[v] >= num[u])
printf("articulation point - %d\n", u);
if (low[v] > num[u])
printf("bridge - (%d, %d)\n", u, v);
low[u] = min(low[u], low[v]);
} else if (par[u] != v) {
// Εδώ υπάρχει back edge.
low[u] = min(low[u], num[v]);
}
}
}
Προσέξτε ότι στη περίπτωση του back edge το low[u] = min(low[u], num[v]) θα μπορούσε να αντικατασταθεί με το low[u] = min(low[u], low[v]) χωρίς να αλλάξει κάτι στην ορθότητα του αλγορίθμου.
Επίσης, αν έχουμε πολλές συνεκτικές συνιστώσες τότε μπορούμε να τρέξουμε την DFS από τυχαίες κορυφές μέχρι να καλύψουμε όλο τον γράφο. Θα δημιουργήσουμε δηλαδή πολλά δέντρα (ένα δάσος). Αυτό μπορεί να γίνει όπως στον παρακάτω κώδικα (μέσα στη main()):
memset(num, -1, sizeof num);
memset(low, -1, sizeof low);
memset(par, -1, sizeof par);
counter = 0;
// Προσέξτε ότι οι κορυφές αριθμούνται ξεκινώντας από το 1
for (int u = 1; u <= n; u++)
if (num[u] == -1)
dfs(u);
Εύκολα βλέπουμε πως ο αλγόριθμος αυτός έχει συνολική χρονική πολυπλοκότητα αφού περνάμε από κάθε κορυφή μία φορά και από κάθε ακμή μία φορά μέσα στην DFS.